<그래프(Graph)>
[그래프에 들어가기에 앞서]
그래프 역시 자료구조이며, 비선형 자료구조에 해당한다.
그리고 트리 때와도 마찬가지로 데이터의 저장보다는 '표현'을 하는데 중점적이다.
실제로 그래프라는 자료구조를 배우게 되면 그래프보다는 그래프와 관련된 알고리즘들을 더 많이 보게 된다.
이는 자료구조에서 저장소의 측면보다는 하나의 '표현 방법'으로 더 많이 사용된다는 것을 의미한다고 볼 수 있다.
그래서 '그래프 자료구조'라는 표현보다는 '그래프 알고리즘'이라는 용어가 더 많이 쓰이게 되고 실제로도 그렇다.
[그래프의 이해와 종류]
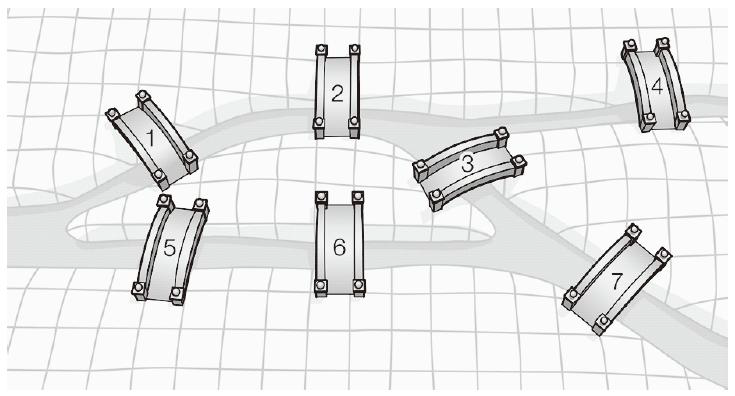
위의 문제는 '쾨니히스베르크의 다리 문제'라는 유명한 문제다.
그리고 이 문제를 풀기 위해서 오일러라는 수학자에 의해 '그래프 이론'이 사용되었다고 한다.
위의 그림을 그래프로 만들면 다음과 같이 표현할 수 있다.
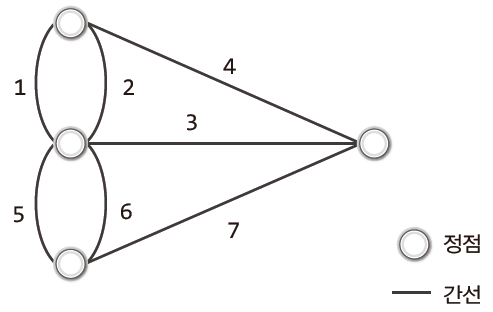
다리와 다리 사이의 강을 경계로 있는 땅을 하나의 점으로, 다리를 선으로 표현하면 위와 같은 그림이 된다.
여기서 점은 '정점(Vertex)'이라고 하며, 선을 '간선(Edge)'이라고 한다.
[무방향 그래프 (Undirected Graph)]
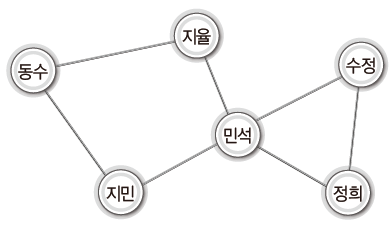
또 다른 예로는 학생들의 비상 연락망이 다음과 같이 구성되었다고 치자.
그러면 '정점'은 각 학생들의 이름이 되고 학생들 사이의 선, 정점 사이의 연결을 '간선'이라고 한다.
현재 이 그래프에는 '방향성'이 빠져있다.
다시 말해서 누가 누구에게 연락을 해야하는지에 대한 정보가 없는 것이다.
위와 같은 그래프를 '무방향 그래프(Undirected Graph)'라고 한다.
[방향 그래프(Directed Graph)]
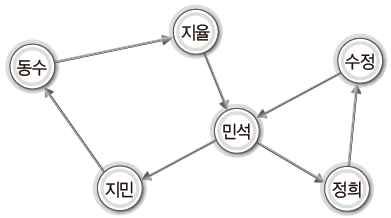
이번 예시는 위와 다르게 누구에게 연락해야 하는지에 대한 방향 정보가 포함되어 있다.
이처럼 간선에 방향 정보가 포함된 그래프를 가리켜 '방향 그래프(Directed Graph)'라고 한다.
다른 말로는 '다이그래프(Digraph)'라고도 한다.
[완전 그래프(Complete Graph)]
위에서 설명한 무방향과 방향 그래프의는 간선의 연결 형태에 따라서 '완전 그래프'로 구분될 수 있다.
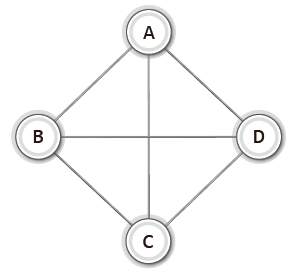
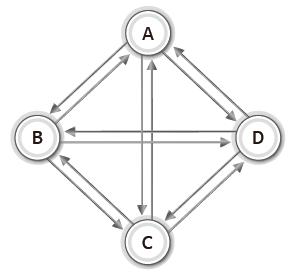
이처럼 모든 정점에 간선이 모두 연결된 그래프를 '완전 그래프(Complete Graph)'라고 한다.
그리고 정점의 수가 동일한 그래프라면 방향 그래프는 무방향 그래프의 간선의 수가 2배가 된다.
[가중치 그래프(Weight Graph)와 부분 그래프(Sub Graph)]
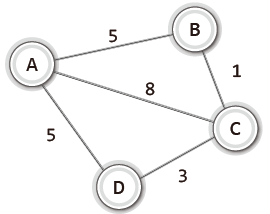
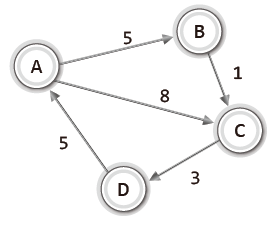
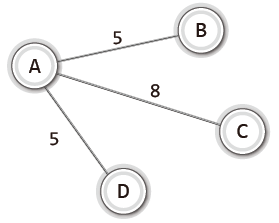
위의 그림처럼 간선에 '가중치 정보'를 두어서 그래프를 구성할 수도 있다.
이러한 유형의 그래프를 '가중치 그래프'라고 한다.
가중치는 두 정점 사이의 거리나 두 정점을 이동하는데 걸리는 시간 등의 정보가 될 수 있다.
만약 가중치가 이동에 걸리는 시간이라고 한다면, A에서 C로 이동하는 최단 거리는 '정점 A-정점B-정점C'가 된다.
그리고 집합에서 부분집합과 유사한 개념으로 '부분 그래프'라는 것이 있다.
부분 집합이 원래 집합의 일부 원소로 이루어진 집합이다.
부분 그래프 역시 원래 그래프의 일부 정점과 간선으로 이뤄진 그래프를 뜻한다.
[그래프의 집합 표현]
그래프는 정점과 간선으로 이뤄져 있으므로, 다음과 같이 정점의 집합과 간선의 집합으로 나눠서 표현할 수 있다.

그래프 G1을 예로 들면 다음과 같이 표현이 가능하다.
그래프 G1의 정점 집합 V(G1) = {A, B, C, D}
그래프 G1의 간선 집합 E(G1) = {(A, B), (A, C), (A, D), (B, C), (C, D)}
무방향 그래프에서는 방향성이 없기 때문에 (A, B)와 (B, A)는 같은 간선을 나타낸다.
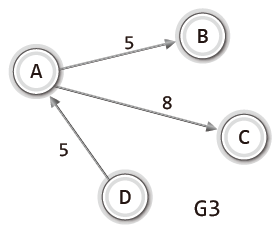
그래프 G3을 예로 들면 다음과 같이 표현이 가능하다.
그래프 G3의 정점 집합 V(G3) = {A, B, C, D}
그래프 G3의 간선 집합 E(G3) = {<A, B>, <A, C>, <D, A>}
무방향 그래프와 달리 방향성이 있으므로 <A, B>와 <B, A>는 같은 간선이 아니다.
[그래프의 ADT]
그래프의 구현을 하기에 앞서, 항상 자료구조를 구현할 때에는 ADT를 정의하고 시작하였다.
여기서 정의하는 그래프의 ADT는 그래프의 구현이 실질적인 목표가 아니다.
그래프를 표현할 수 있게 하는 것이 목적이다.
그리고 이후 표현된 그래프를 이용한 탐색이나 알고리즘 등에 더 중점을 둬야한다.
탐색 방법이나 알고리즘에 따라서 구성될 수 있는 그래프는 달라질 수 있기 때문이다.
그래서 그래프의 구성을 위한 ADT는 필요한 만큼만 제한적으로 정의를 한다.
[그래프 자료구조의 ADT]
void GraphInit(ALGraph* pg, int nv);
- 그래프의 초기화.
- 두 번째 인자로 정점의 수를 입력받는다.
void GraphDestroy(ALGraph* pg);
- 그래프 초기화 과정에서 할당한 리소스를 반환(할당 해제)한다.
void AddEdge(ALGraph* pg, int fromV, int toV);
- 매개변수 fromV와 toV로 전달된 정점을 연결하는 간선을 그래프에 추가한다.
void ShowGraphEdgeInfo(ALGraph* pg);
- 그래프의 간선 정보를 출력한다.
위의 ADT에서는 그래프의 초기화 과정에서 정점의 수를 결정하도록 정의를 하였다.
그리고 간선을 추가는 하지만 삭제는 할 수 없도록 정의가 된 상태다.
여기서 정점에 이름을 어떻게 부여할 것인가에 대해서는 열거형 상수를 활용할 수 있다.
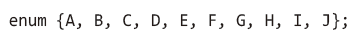
위처럼 정점의 이름을 상수화할 수 있다.
그래서 초기화 함수를 호출할 때, 두 번째 인자에 5를 전달하면 A, B, C, D, E의 정점을 가진 그래프가 형성된다.
그리고 이 상수들을 간선을 추가하는 함수를 호출할 때, fromV와 toV의 인자로 전달할 수 있다.
이제 ADT를 정의했으니 헤더파일을 정의해야 한다.
하지만 그 전에 그래프를 구현하는 방법에 대해서 생각해야 한다.
그래프를 어떤 방식으로 구현하는가에 따라서 헤더 파일의 구성도 달라지기 때문이다.
[그래프를 구현하는 두 가지 방법]
그래프를 구현하는 방법은 크게 두 가지 방법이 있다.
1) 인접 행렬(Adjacent Matrix) 기반 그래프
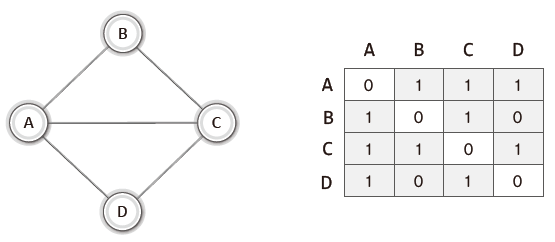
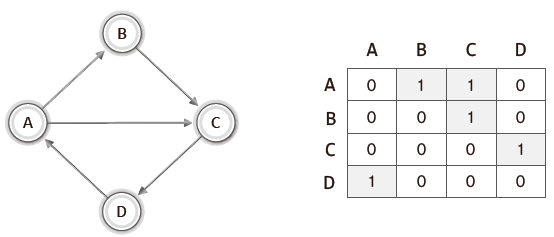
정방 행렬(2차원 배열, NxN 배열)을 활용하는 방식이다.
2) 인접 리스트(Adjacent List) 기반 그래프
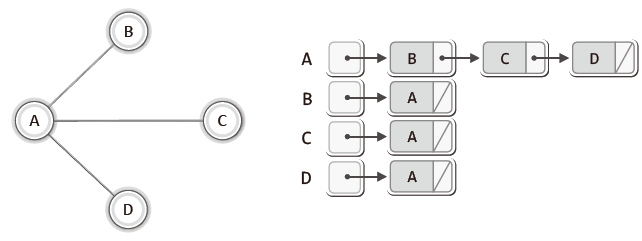
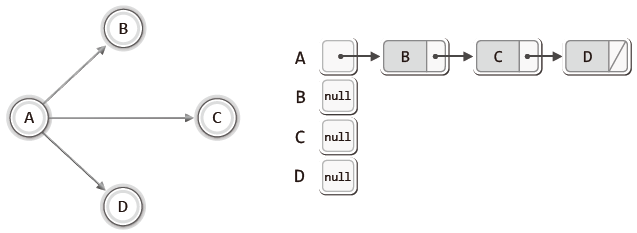
연결 리스트를 활용하는 방식이다.
[구현]
[SingleLinkedList.h]
/*
* 선형 자료구조 - 단일 연결 리스트 (더미 노드 기반)
* 파일명: SingleLinkedList.h
* 파일 버전: 0.3
* 작성자: Sevenshards
* 작성 일자: 2023-11-30
* 이전 버전 작성 일자: 2023-11-29
* 버전 내용: 정렬 기준 삽입 추가
* 이전 버전 내용: 해시 충돌 문제 해결을 위한 체이닝 기법 구현
*/
#ifndef __SINGLE_LINKED_LIST_H__
#define __SINGLE_LINKED_LIST_H__
#define TRUE 1 // 참일 경우 1
#define FALSE 0 // 거짓일 경우 0
typedef int LData; // 어떤 데이터를 쓸지 모르니 일단은 LData로 매크로 지정, 편의상 int
typedef int CompareFunc(LData d1, LData d2);
typedef struct _node
{
LData data; // 노드에 담길 데이터
struct _node* next; // 다음 노드를 가리키기 위한 포인터
} Node;
typedef struct _linkedlist
{
Node* head; // head를 가리키는 포인터
Node* cur; // 현재 참조하는 위치를 가리키는 포인터
Node* before; // 현재보다 하나 앞의 위치를 가리키는 포인터
int numOfData; // 현재 저장된 데이터 수를 확인하기 위해 사용
CompareFunc* comp; // 정렬 기준 함수를 가리키기 위한 함수 포인터
} LinkedList;
typedef LinkedList List;
void ListInit(List* plist); // 리스트의 초기화에 사용
void FInsert(List* plist, LData data); // 정렬 기준 없이 리스트의 노드를 생성할 때 사용
void SInsert(List* plist, LData data); // 정렬 기준에 맞춰서 리스트의 노드를 생성할 때 사용
void LInsert(List* plist, LData data); // 리스트의 노드를 새로 생성할 때 사용
int LFirst(List* plist, LData* pdata); // 리스트의 맨 첫번째 데이터를 참조할 때 사용
int LNext(List* plist, LData* pdata); // LFirst 이후의 데이터를 참조할 때 사용
LData LRemove(List* plist); // LFirst, LNext가 참조한 데이터를 삭제하고 메모리 해제에 사용, 연속 호출 불가
int LCount(List* plist); // 현재 리스트에 저장된 노드 수 확인
void SetSortRule(List* plist, CompareFunc pcomp); // 리스트에 정렬 기준 함수를 등록
#endif[SingleLinkedList.c]
/*
* 선형 자료구조 - 단일 연결 리스트 (더미 노드 기반)
* 파일명: SingleLinkedList.c
* 파일 버전: 0.3
* 작성자: Sevenshards
* 작성 일자: 2023-11-30
* 이전 버전 작성 일자: 2023-11-29
* 버전 내용: 정렬 기준 삽입 추가 및 로직 수정
* 이전 버전 내용: 해시 충돌 문제 해결을 위한 체이닝 기법 구현
*/
#include <stdlib.h>
#include "SingleLinkedList.h"
// 리스트의 초기화에 사용
void ListInit(List* plist)
{
plist->head = (Node*)malloc(sizeof(Node)); // 더미 노드를 바로 가리키게 한다.
plist->head->next = NULL; // 더미 노드가 가리키는 다음을 NULL로
plist->numOfData = 0; // 그리고 더미노드를 제외하고 실제 데이터 수를 기록해야하므로 0이다. -1이 아니다.
plist->comp = NULL; // 초기화시 우선순위 판별을 위한 함수는 미지정된 상태이므로 NULL
}
void FInsert(List* plist, LData data) // 정렬 기준 없이 리스트의 노드를 생성할 때 사용
{
Node* newNode = (Node*)malloc(sizeof(Node)); // 새로운 노드 메모리 할당
newNode->data = data; // 노드에 데이터 입력
newNode->next = plist->head->next; // head부터 데이터가 들어가기 때문에, 더미노드 다음을 가리키고 있는 것을 새로운 노드가 가리키게 해야함
plist->head->next = newNode; // head에서부터 들어가므로 더미노드 다음을 새로운 노드를 가리키게 함
(plist->numOfData)++; // 데이터 수 증가
}
// 정렬 기준에 맞춰서 리스트의 노드를 생성할 때 사용 (Sort Insert)
void SInsert(List* plist, LData data)
{
Node* newNode = (Node*)malloc(sizeof(Node)); // 새로운 노드 메모리 할당
newNode->data = data; // 노드에 데이터 입력
Node* cur = plist->head; // 삽입을 위해 사용하는 현재 위치(current), 시작 위치는 더미노드
// 새 노드가 들어갈 위치를 찾기 위한 반복문 수행
// 더 이상 읽을 노드가 없을 때까지, 그리고 새 노드에 들어갈 데이터와 기존 노드의 데이터를 비교하여 기준에 맞을 때까지 반복
while (cur->next != NULL && plist->comp(data, cur->next->data) != 0)
{
cur = cur->next; // 정렬 기준에 맞는 위치까지 다음 노드로 이동
}
// 반복문이 끝났다면 노드를 삽입할 위치(cursor)를 찾은 것
newNode->next = cur->next; // cur의 다음 위치에 새로운 노드가 들어가기 때문에, cur의 다음을 새로운 노드가 가리키도록 해야함
cur->next = newNode; // 그리고 cur의 next를 새로운 노드를 가리키게 함
(plist->numOfData)++; // 데이터 수 증가
}
// 리스트의 노드를 새로 생성할 때 사용
void LInsert(List* plist, LData data)
{
if (plist->comp == NULL) // 정렬 기준이 없다면
FInsert(plist, data); // FInsert 호출
else // 정렬 기준이 있다면
SInsert(plist, data); // SInsert 호출
}
// 리스트의 맨 첫번째 데이터를 참조할 때 사용
int LFirst(List* plist, LData* pdata)
{
// 쓸 필요 없었음. 매개변수 있으므로 그거 쓰면 됨
// LData nData; // 노드의 데이터를 받기 위한 변수
if (plist->head->next == NULL) // 만약 더미노드 이후에 가리키는 노드가 없다면
return FALSE; // 데이터가 없다
plist->cur = plist->head->next; // 현재 위치를 다음 노드를 가리키게 한다
plist->before = plist->head; // 그리고 before는 현재 위치 앞인 더미노드를 가리킨다
*pdata = plist->cur->data; // 현재 위치의 데이터를 참조
return TRUE; // 데이터 참조에 성공했다
}
// LFirst 이후의 데이터를 참조할 때 사용
int LNext(List* plist, LData* pdata)
{
// 마찬가지로 쓸 필요 없었음. 매개변수 있으므로 그거 쓰면 됨
// LData nData; // 노드의 데이터를 받기 위한 변수
if (plist->cur->next == NULL) // 현재 위치 다음이 가리키는 노드가 없다면
return FALSE; // 데이터가 없다
plist->before = plist->cur; // before에 현재 가리키는 노드 위치를 저장
plist->cur = plist->cur->next; // 현재 가리키는 위치를 하나 앞으로 이동
*pdata = plist->cur->data; // 현재 가리키는 위치의 데이터 참조 -> 데이터 참조 위치를 잘못 지정하였음
return TRUE; // 데이터 참조 성공
}
// LFirst, LNext가 참조한 데이터를 삭제하고 메모리 해제에 사용, 연속 호출 불가
LData LRemove(List* plist)
{
LData rdata; // 지워질 노드의 데이터
Node* rNode; // 현재 참조 중인, 지워질 노드를 담기 위한 노드 포인터
rdata = plist->cur->data; // 현재 지워질 데이터를 담고
rNode = plist->cur; // 지워질 노드는 현재 참조중인 노드를 가리킨다
plist->before->next = plist->cur->next; // 그리고 이전 노드와 현재 가리키는 노드의 뒤를 연결
plist->cur = plist->before; // 그리고 현재 참조중인 위치를 하나 앞으로 옮긴다
free(rNode); // 여기서 메모리를 해제해주고
(plist->numOfData)--; // 데이터 수 감소
return rdata; // 데이터를 반환한다.
}
// 현재 리스트에 저장된 노드 수 확인
int LCount(List* plist)
{
return plist->numOfData;
}
// 리스트에 정렬 기준 함수를 등록
void SetSortRule(List* plist, CompareFunc pcomp)
{
plist->comp = pcomp;
}[ALGraph.h]
/*
* 비선형 자료구조 - 인접 리스트(Adjacent List) 기반 무방향 그래프
* 파일명: ALGraph.h
* 파일 버전: 0.1
* 작성자: Sevenshards
* 작성 일자: 2023-11-30
* 이전 버전 작성 일자:
* 버전 내용: 간단한 인접 리스트 기반 무방향 그래프 구현
* 이전 버전 내용:
*/
#ifndef __ALGRAPH_H__
#define __ALGRAPH_H__
// 인접 리스트 기반으로 구현을 하므로 단일 연결 리스트를 사용
#include "SingleLinkedList.h"
// 정점의 이름을 상수화
// A는 0으로 초기화되어 1씩 증가
enum {A, B, C, D, E, F, G, H, I, J};
// 무방향 인접 리스트(Undirected Adjacent List) 그래프 구조체
typedef struct _ual
{
int numVertex; // 정점의 수
int numEdge; // 간선의 수
List* adjList; // 간선의 정보(어떤 정점과 연결되었는지에 대한 정보)
} ALGraph;
// 그래프 자료구조의 ADT
// 초기화
void GraphInit(ALGraph* pg, int nv);
// 그래프의 리소스 해제 (삭제)
void GraphDestroy(ALGraph* pg);
// 간선 추가(연결)
void AddEdge(ALGraph* pg, int fromV, int toV);
// 간선 정보 출력
void ShowGraphEdgeInfo(ALGraph* pg);
#endif[ALGraph.c]
/*
* 비선형 자료구조 - 인접 리스트(Adjacent List) 기반 무방향 그래프
* 파일명: ALGraph.h
* 파일 버전: 0.1
* 작성자: Sevenshards
* 작성 일자: 2023-11-30
* 이전 버전 작성 일자:
* 버전 내용: 간단한 인접 리스트 기반 무방향 그래프 구현
* 이전 버전 내용:
*/
#include <stdio.h>
#include <stdlib.h>
#include "ALGraph.h"
// 인접 리스트 기반으로 구현을 하므로 단일 연결 리스트를 사용
#include "SingleLinkedList.h"
// 저자는 출력의 형태를 좋게 하기 위해서 정렬 기준(우선순위 판별)을 넣었다.
// 사실 넣어도 그만이고 안넣어도 그만인 부분이다.
// 혹시라도 이 미흡한 코드를 보고 따라한다면 이 함수는 빼도 된다.
int WhoisPrecede(int d1, int d2)
{
// 오름차순 정렬
if (d1 < d2)
return 0; // d1의 우선 순위가 앞선다면 0을
else
return 1; // d2의 우선 순위가 앞서거나 같다면 1을
}
// 그래프 자료구조의 ADT
// 초기화
void GraphInit(ALGraph* pg, int nv)
{
pg->adjList = (List*)malloc(sizeof(List) * nv); // 정점의 수만큼 메모리 할당
pg->numVertex = nv; // 입력받은 nv는 정점의 수
pg->numEdge = 0; // 초기화시 간선의 수는 0
int i; // 반복문에서 사용할 변수 i
for (i = 0; i < nv; i++)
{
ListInit(&(pg->adjList[i])); // 정점의 수만큼 List 초기화
SetSortRule(&(pg->adjList[i]), WhoisPrecede); // 각 List에 정렬 기준 함수 등록 -> 정렬 기준을 안쓴다면 빼도 됨
}
}
// 그래프의 리소스 해제 (삭제)
void GraphDestroy(ALGraph* pg)
{
if (pg->adjList != NULL)
free(pg->adjList);
}
// 간선 추가(연결)
void AddEdge(ALGraph* pg, int fromV, int toV)
{
LInsert(&(pg->adjList[fromV]), toV); // from->to
LInsert(&(pg->adjList[toV]), fromV); // to->from
pg->numEdge += 1;
}
// 간선 정보 출력
void ShowGraphEdgeInfo(ALGraph* pg)
{
int i; // 반복문에 사용할 변수 i
int vertex; // 정점
for (i = 0; i < pg->numVertex; i++)
{
printf("%c와 연결된 정점: ", i + 65); // 아스키 코드 65가 'A'
if (LFirst(&(pg->adjList[i]), &vertex))
{
printf("%c ", vertex += 65);
while(LNext(&(pg->adjList[i]), &vertex))
printf("%c ", vertex += 65);
}
printf("\n");
}
}[ALGraphMain.c]
/*
* 비선형 자료구조 - 인접 리스트(Adjacent List) 기반 무방향 그래프
* 파일명: ALGraphMain.c
* 파일 버전: 0.1
* 작성자: Sevenshards
* 작성 일자: 2023-11-30
* 이전 버전 작성 일자:
* 버전 내용: 간단한 인접 리스트 기반 무방향 그래프 구현
* 이전 버전 내용:
*/
#include <stdio.h>
#include "ALGraph.h"
int main()
{
ALGraph graph; // 그래프 생성
GraphInit(&graph, 5); // 그래프 초기화
// 정점 연결 (간선 추가)
AddEdge(&graph, A, B);
AddEdge(&graph, A, D);
AddEdge(&graph, B, C);
AddEdge(&graph, C, D);
AddEdge(&graph, D, E);
AddEdge(&graph, E, A);
ShowGraphEdgeInfo(&graph);
GraphDestroy(&graph);
return 0;
}
구현은 연결 리스트 방식을 활용하여 구현을 하였다.
그래서 기존에 구현했었던 더미 노드 기반의 단일 연결 리스트를 사용.
그 외에 그래프를 구현하는 코드는 크게 어렵지 않다.
코드에 주석을 충분히 달아뒀으므로 나중에 코드를 보면서 복습을 해도 이해하기 쉬운 수준이다.