[자료구조, C] AVL 트리 구현

<AVL 트리>

[이진 탐색 트리의 문제점과 AVL 트리]

이진 탐색 트리의 탐색 연산은 $O(log_2n)$의 시간 복잡도를 가진다.
이는 이진 트리가 가지는 특징이며 트리의 높이가 하나씩 늘어날수록 추가되는 노드의 수가 2배 증가하기 때문이다.
그런데 이진 탐색 트리는 균형이 맞지 않을수록 $O(n)$에 가까운 시간 복잡도를 가지게 된다.
이를테면 1부터 5까지 순서대로 이진 탐색 트리에 삽입한다고 가정하자.

 

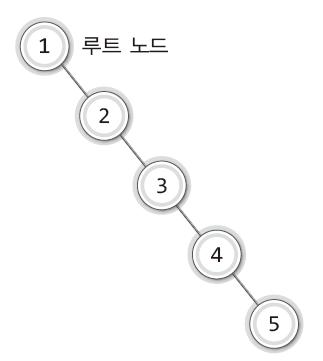
그러면 1이 루트노드가 되고 오른쪽으로만 길게 쭉 늘어진 이진 탐색 트리가 된다.
이는 선형 자료구조와 다를 바가 없는 모양이 된다.

 

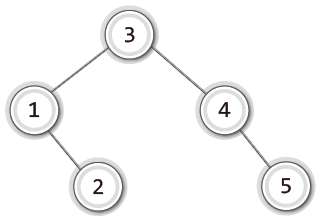
저장 순서를 조금만 바꿔서 3을 먼저 저장하면 균형이 괜찮게 잡히게 된다.
저장 순서만 바뀌어도 탐색의 성능에 큰 차이를 보이는 것이 이진 탐색 트리의 단점이다.
그리고 이와 같은 단점을 해결한 트리를 ‘균형 잡힌 이진 트리’라 하며, 다음과 같은 종류가 있다.

AVL 트리 / 2-3 트리 / 2-3-4 트리 / Red-Black 트리 / B-트리

[자동으로 균형을 잡는 AVL 트리와 균형 인수]

AVL 트리는 노드가 추가, 삭제될 때 트리의 균형 상태를 파악해서 스스로 그 구조를 변경하여 균형을 잡는 트리다.
그리고 그 균형의 정도를 표현하기 위해 균형 인수(Balance Factor)라는 것을 사용한다.
균형 인수는 다음과 같이 계산된다.

균형인수 = 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이

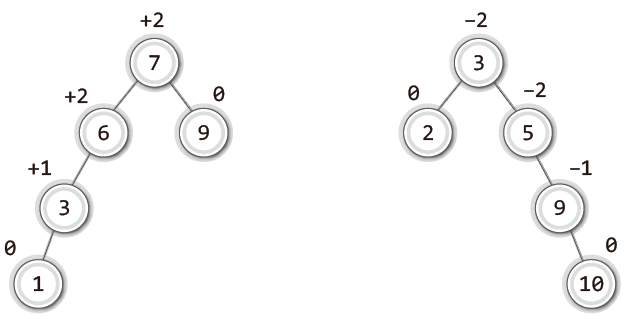
AVL 트리는 균형 인수의 절댓값이 2 이상인 경우에 균형이 무너졌다고 판단하고, 트리의 구조를 재조정하게 된다.
이때 트리의 구조를 재조정하는 것을 ‘리밸런싱(Rebalancing)’이라고 한다.
그리고 균형이 무너졌다는 것은 쉽게 표현하면 트리의 높이가 불필요하게 커진 상황을 뜻한다.
바꿔서 말하면 높이를 낮출 수 있는 상황이라고 볼 수 있다.

[리밸런싱 4총사 - LL, RR, LR, RL]

AVL 트리에서 균형이 무너지는 경우는 4가지로 LL, RR, LR, RL 상태로 나뉘게 된다.
그리고 각 상태 별 리밸런싱 방법도 차이가 있다.

1) LL상태와 LL회전

 

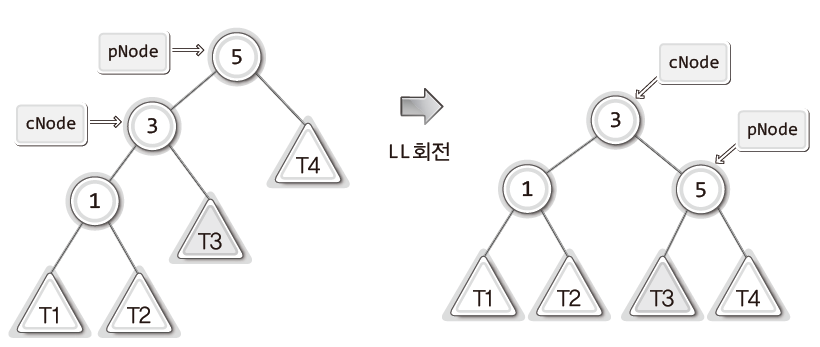
LL상태는 자식 노드가 왼쪽으로 연달아 연결되어 균형 인수 +2가 된 상태를 말한다.
이와 같은 불균형 상태를 ‘Left Left 상태’라고 하며 줄여서 ‘LL 상태’ 라고 한다.
그리고 LL 상태로 인한 불균형을 해소하기 위해 사용하는 것이 ‘LL 회전’이다.

2) RR상태와 RR회전

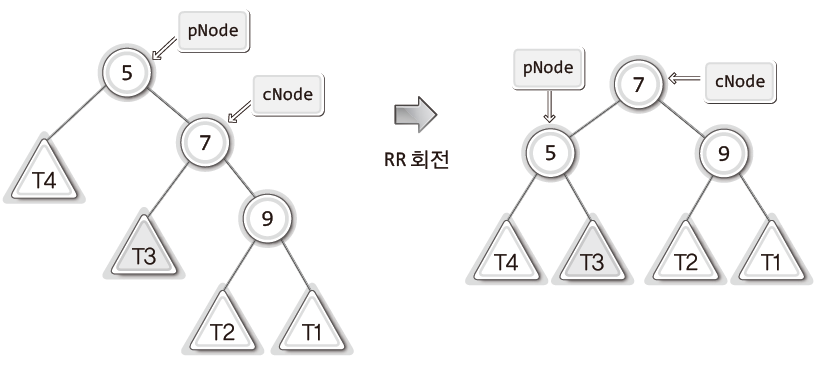
RR상태는 LL상태와 방향이 바뀐 상황이다.
자식 노드가 오른쪽으로 연달아 연결되어 균형 인수가 -2가 된 상태를 말한다.
마찬가지로 이와 같은 불균형 상태를 ‘Right Right 상태’라고 하며, 줄여서 ‘RR 상태’라고 한다.
그리고 RR 상태로 인한 불균형을 해소하기 위해 사용하는 것이 ‘RR 회전’이다.

3) LR상태와 LR회전

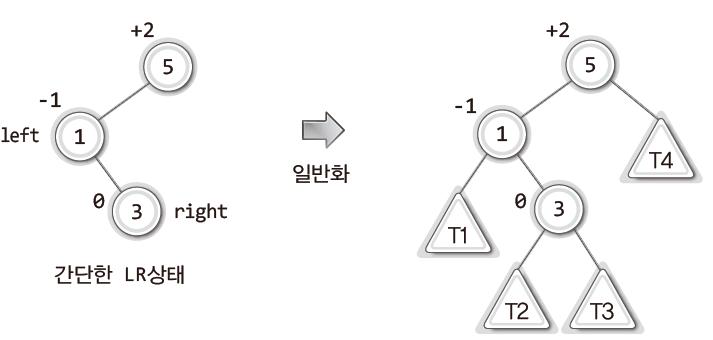
LR상태는 LL 상태처럼 균형인수가 +2인 상태지만 약간 다른 부분이 있다.
루트 노드의 왼쪽(L)에 자식 노드가 있고, 그 자식 노드의 오른쪽(R)에 자식 노드가 있는 상황이다.
그래서 루트 노드를 기준으로는 균형 인수가 +2가 된 상태고, 이를 ‘LR 상태’라고 한다.
LR 상태는 LL이나 RR 상태처럼 한 번의 회전으로는 균형을 잡을 수가 없다.
따라서 다음과 같은 방법을 취해야 한다.

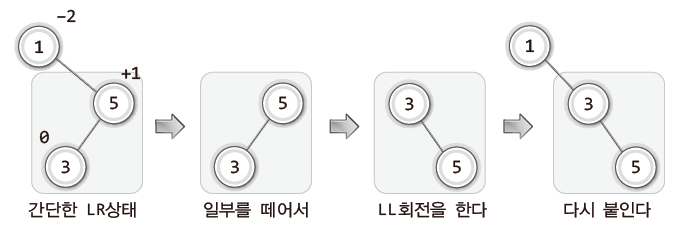
“LR 상태를 한 번의 회전으로 균형을 잡을 수 있는 LL 또는 RR 상태로 만들어야 한다”

LR 상태에서 LL상태로 만들기 위해 부분 RR회전 (LR회전 과정 - 1)

그리고 나서 LL 회전 (LR 회전 과정 - 2)

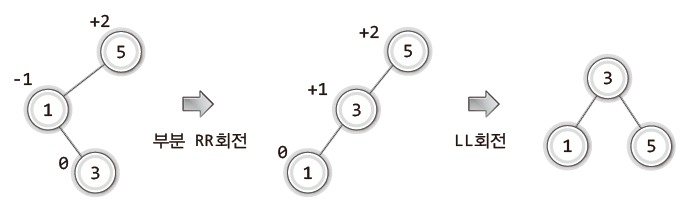
LR 상태는 LL 상태로 만든 이후 LL 회전을 통해 불균형을 해소한다.

4) RL상태와 RL회전

RL상태는 LR 상태와 방향만 다를 뿐 원리는 똑같다.
루트 노드의 오른쪽(R)에 자식 노드가 있고, 그 자식 노드의 왼쪽(L)에 자식 노드가 있는 상황이다.
그래서 루트 노드를 기준으로는 균형 인수가 -2가 된 상태고, 이를 ‘RL 상태’라고 한다.
마찬가지로 RL 상태는 LL이나 RR 상태처럼 한 번의 회전으로는 균형을 잡을 수가 없다.
따라서 다음과 같은 방법을 취해야 한다.
“RL 상태를 한 번의 회전으로 균형을 잡을 수 있는 LL 또는 RR 상태로 만들어야 한다”

RL 상태에서 RR상태로 만들기 위해 부분 LL회전 (RL회전 과정 - 1)

그리고 나서 RR 회전 (RL 회전 과정 - 2)

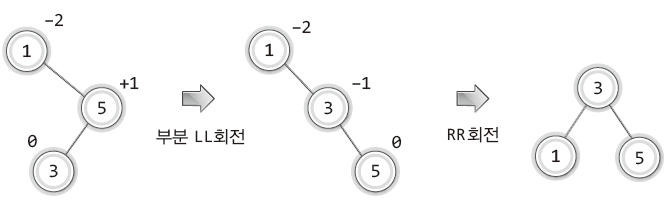
RL 상태는 RR 상태로 만든 이후 RR 회전을 통해 불균형을 해소한다.

[구현]

https://sevenshards.tistory.com/7

[자료구조, C] 양방향 연결 리스트 기반 이진 트리 구현

https://sevenshards.tistory.com/25

[자료구조, C] 이진 탐색 트리(Binary Search Tree) 구현

기존에 사용했던 이진 트리와 이진 탐색 트리의 코드를 활용하되, 이진 탐색 트리 부분의 코드는 확장을 한다.
AVL 트리 역시 이진 탐색 트리의 일종이므로 이전에 구현했던 이진 트리와 이진 탐색 트리를 활용할 수 있다.
확장을 하면서 바뀌는 부분은 BinarySearchTree.c에서 BSTInsert와 BSTRemove의 정의를 바꾸게 된다.
트리의 균형이 깨지는 순간은 탐색이 아닌 삽입과 삭제에서 발생하기 때문이다.
그리고 별도로 리밸런싱을 위한 도구를 만들기 위해 AVLRebalance.h와 AVLRebalance.c를 추가한다.

 

[BinarySearchTree.c]

/*
* 비선형 자료구조 - 연결 리스트 기반 이진 탐색 트리
* 파일명: BinarySearchTree.c
* 파일 버전: 0.3
* 작성자: Sevenshards
* 작성 일자: 2023-11-29
* 이전 버전 작성 일자: 2023-11-28
* 버전 내용: AVL 트리 확장에 따른 삽입, 삭제 부분 수정
* 이전 버전 내용: 삭제 기능, 트리 전체 조회 추가로 구현
*/
#include <stdlib.h>
#include "BinarySearchTree.h"
#include "AVLRebalance.h"

// 이진 탐색 트리의 생성 및 초기화
void BSTMakeAndInit(BTreeNode** pRoot)
{
	*pRoot = NULL;
}

// 노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode* bst)
{
	return bst->data;
}

// 이진 탐색 트리를 대상으로 데이터 저장 (노드 생성 포함)
// 재귀 형태로 변경하여 구현
// 반환형으로 BTreeNode*를 반환. -> 자기 참조 가능.
// 이 부분은 객체 지향 공부하면서 다시 보면 좋을듯 하여 void로 놓지 않았음
BTreeNode* BSTInsert(BTreeNode** pRoot, BSTData data)
{
	if (*pRoot == NULL) // 노드가 추가될 위치를 찾은 상황 (재귀의 탈출 조건)
	{
		*pRoot = MakeBTreeNode(); // 새로운 노드를 생성하고
		SetData(*pRoot, data); // 새로운 노드에 데이터를 저장
	}
	else if (data < GetData(*pRoot)) // 새로 저장될 데이터가 현재 가리키는 노드보다 작다면
	{
		BSTInsert(&((*pRoot)->left), data); // 왼쪽에 추가하기 위한 BSTInsert 호출 (재귀)
		*pRoot = Rebalance(pRoot); // 노드 추가가 끝난 이후 Rebalance 호출을 통한 리밸런싱
	}
	else if (data > GetData(*pRoot)) // 새로 저장될 데이터가 현재 가리키는 노드보다 크다면
	{
		BSTInsert(&((*pRoot)->right), data); // 오른쪽에 추가하기 위한 BSTInsert 다시 호출 (재귀)
		*pRoot = Rebalance(pRoot); // 노드 추가가 끝난 이후 Rebalance 호출을 통한 리밸런싱
	}
	else // 그 이외의 경우는 Key의 값이 같은 경우 하나.
	{
		return NULL; // 이진 탐색 트리에서 Key는 중복을 허용하지 않으므로 NULL 반환
	}

	return *pRoot;
}

// 이진 탐색 트리를 대상으로 데이터 탐색
BTreeNode* BSTSearch(BTreeNode* bst, BSTData target)
{
	BTreeNode* cNode = bst; // 현재(current) 가리키는 노드, 트리의 주소값(루트 노드의 주소값)부터 시작한다.
	BSTData cData; // 현재 가리키는 노드의 데이터 값

	// 현재 가리키는 노드가 NULL이 아닐때까지
	while (cNode != NULL)
	{
		cData = GetData(cNode);

		if (target == cData) // 대상을 찾았다면
			return cNode; // 현재 가리키는 노드의 주소값 반환
		else if (target < cData) // 찾는 값이 현재 노드의 데이터보다 작다면
			cNode = GetLeftSubTree(cNode); // 왼쪽으로 이동
		else // 찾는 값이 현재 노드의 데이터보다 크다면
			cNode = GetRightSubTree(cNode);
	}

	return NULL; // 탐색 대상이 아예 없는 경우, NULL을 반환
}

// 트리에서 노드를 제거하고 제거된 노드의 주소값을 반환
BTreeNode* BSTRemove(BTreeNode** pRoot, BSTData target)
{
	// 삭제 대상이 루트 노드일 경우도 고려하여 진행
	BTreeNode* pVRoot = MakeBTreeNode(); // 가상 루트 노드 (Virtual Root Node) - 저자가 쓴 꼼수(?)
	BTreeNode* pNode = pVRoot; // 현재 가리키는 노드의 부모 노드, 초기화 하면서 가상의 루트 노드를 가리킨다
	BTreeNode* cNode = *pRoot; // 현재(current) 가리키는 노드, 초기화 하면서 루트 노드를 가리킨다
	BTreeNode* dNode = NULL; // 지워질 대상의 노드, 일부 컴파일러에서는 초기화하지 않으면 에러를 띄우므로 NULL로 초기화

	// 루트 노드를 pVRoot가 가리키고 있는 노드의 오른쪽 자식 노드가 되게 한다.
	ChangeRightSubTree(pVRoot, *pRoot);

	// 삭제 대상이 될 노드를 탐색
	while (cNode != NULL && GetData(cNode) != target)
	{
		pNode = cNode; // 현재 노드 위치를 현재 위치한 노드의 부모 노드로 갱신

		if (target < GetData(cNode)) // 삭제할 데이터가 현재 노드의 데이터보다 작다면
			cNode = GetLeftSubTree(cNode); // 왼쪽으로 이동
		else // 삭제할 데이터가 현재 노드의 데이터보다 크다면
			cNode = GetRightSubTree(cNode); // 오른쪽으로 이동
	}

	if (cNode == NULL) // 삭제 대상이 없다면
		return NULL; // NULL을 return

	dNode = cNode; // 삭제 대상을 dNode가 가리키게 함

	// 1번 케이스: 삭제 대상이 단말 노드라면
	if (GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL) // 양쪽에 자식 노드가 둘 다 없으므로
	{
		if (GetLeftSubTree(pNode) == dNode) // 만약 삭제할 노드의 부모 노드의 왼쪽 노드라면
			RemoveLeftSubTree(pNode); // 부모 노드의 왼쪽 노드를 삭제
		else // 오른쪽 노드라면
			RemoveRightSubTree(pNode); // 부모 노드의 오른쪽 노드를 삭제
	}

	// 2번 케이스: 삭제 대상이 자식 노드를 하나 갖는 경우
	else if (GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL) // 삭제할 노드의 왼쪽 또는 오른쪽에 자식 노드가 있다면
	{
		BTreeNode* dcNode; // 삭제 대상 노드의 자식(child) 노드를 가리키기 위해 사용할 BTreeNode* 변수

		if (GetLeftSubTree(dNode) != NULL) // 삭제할 노드의 왼쪽에 자식 노드가 있다면
			dcNode = GetLeftSubTree(dNode); // dcNode가 삭제할 노드의 왼쪽 자식을 가리키게 한다.
		else // 삭제할 노드의 오른쪽에 자식 노드가 있다면
			dcNode = GetRightSubTree(dNode); //dcNode가 삭제할 노드의 오른쪽 자식을 가리키게 한다.

		if (GetLeftSubTree(pNode) == dNode) // 만약 삭제할 노드의 부모 노드의 왼쪽 노드라면
			ChangeLeftSubTree(pNode, dcNode); // 부모 노드의 왼쪽을 삭제할 노드의 자식 노드로 바꾼다.
		else // 오른쪽 노드라면
			ChangeRightSubTree(pNode, dcNode); // 부모 노드의 오른쪽을 삭제할 노드의 자식 노드로 바꾼다.
	}

	// 3번 케이스: 삭제 대상이 양쪽 다 자식 노드를 갖는 경우
	// 이 경우에는 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값을 지니는 노드를 찾는다.
	// 그리고 가장 작은 값을 지니는 노드를 삭제할 노드를 대체한다.
	else
	{
		BTreeNode* mNode = GetRightSubTree(dNode); // 대체할 노드를 가리킨다. 오른쪽 서브트리에서 가장 작은 값을 찾아야 하니 오른쪽 자식 노드 값으로 초기화
		BTreeNode* mpNode = dNode; // 대체할 노드의 부모 노드. 삭제할 노드를 가리키는 것으로 초기화
		int delData; // 삭제할 노드의 데이터를 받기 위한 변수

		// 삭제 노드를 대체할 노드를 찾는다.
		while (GetLeftSubTree(mNode) != NULL) // 가장 작은 값을 찾는 것이므로 계속 왼쪽 서브트리만 찾으면 됨. NULL을 만나면 더 이상 없는 것.
		{
			mpNode = mNode; // 대체할 노드의 부모 노드 갱신
			mNode = GetLeftSubTree(mNode); // 대체할 노드를 찾기 위해 왼쪽 자식 노드로 갱신
		}

		// 대체할 노드를 찾은 후
		// 대체 노드에 저장된 값을 삭제할 노드에 대입
		delData = GetData(dNode); // 삭제할 노드에 있는 값을 받는다. (백업)
		SetData(dNode, GetData(mNode)); // 삭제할 노드에 있는 값을 대체할 노드의 값으로 변경

		// 대체할 노드의 부모 노드와 대체 노드의 자식 노드를 연결한다.
		if (GetLeftSubTree(mpNode) == mNode) // 대체할 노드의 부모 노드의 왼쪽 자식 노드가 대체할 노드라면
			ChangeLeftSubTree(mpNode, GetRightSubTree(mNode)); // 대체할 노드의 자식 노드를 왼쪽 자식 노드로 연결
		else // 대체할 노드의 부모 노드의 오른쪽 자식 노드가 대체할 노드라면
			ChangeRightSubTree(mpNode, GetRightSubTree(mNode)); // 대체할 노드의 자식 노드를 오른쪽 자식 노드로 연결

		dNode = mNode; // 삭제할 노드를 대체할 노드로 변경
		SetData(dNode, delData); // 삭제할 노드가 가지고 있던 데이터를 다시 입력
	}

	// 삭제된 노드가 루트 노드일 경우에 대한 추가 처리
	if (GetRightSubTree(pVRoot) != *pRoot) // 가상 루트 노드의 오른쪽 자식 노드가 루트노드가 아니라면
		*pRoot = GetRightSubTree(pVRoot); // 루트 노드가 바뀐 것이므로 가상 루트 노드의 오른쪽 자식을 루트노드로 변경

	free(pVRoot); // 가상 루트 노드의 소멸
	*pRoot = Rebalance(pRoot); 	// 노드 제거 후 리밸런싱
	return dNode; // 삭제 노드의 주소값 반환
}

// int형 데이터의 출력을 위한 함수
void ShowIntData(int data)
{
	printf("%d ", data);
}

// 이진 탐색 트리에 저장된 모든 노드의 데이터 출력
void BSTShowAll(BTreeNode* bst)
{
	InorderTraversal(bst, ShowIntData);
}

삽입 부분에서 좀 더 신경을 써야하는 부분이 있다.
노드 삭제의 경우에는 노드가 하나 삭제가 되고 난 이후에 균형이 잡혀있는지에 대한 여부를 판단한다.
하지만 노드 삽입의 경우에는 오른쪽이나 왼쪽, 또는 삽입이 되는 경우마다 균형이 잡히는지 여부를 판단해야 한다.
그래서 기존의 코드를 변경하여 재귀적으로 삽입을 하는 코드로 변경하여 구현하였다.

[AVLRebalance.h]

/*
* 비선형 자료구조 - AVL 트리 (이진 탐색 트리 확장)
* 파일명: AVLRebalance.h
* 파일 버전: 0.1
* 작성자: Sevenshards
* 작성 일자: 2023-11-29
* 이전 버전 작성 일자:
* 버전 내용: 균형을 잡는 이진 탐색 트리인 AVL 트리 확장 구현
* 이전 버전 내용:
*/

#ifndef __AVL_REBALANCE_H__
#define __AVL_REBALANCE_H__

#include "BinaryTree.h"

// 트리의 균형을 잡는 함수
BTreeNode* Rebalance(BTreeNode** pRoot);

#endif

 

[AVLRebalance.c]

/*
* 비선형 자료구조 - AVL 트리 (이진 탐색 트리 확장)
* 파일명: AVLRebalance.c
* 파일 버전: 0.1
* 작성자: Sevenshards
* 작성 일자: 2023-11-29
* 이전 버전 작성 일자:
* 버전 내용: 균형을 잡는 이진 탐색 트리인 AVL 트리 확장 구현
* 이전 버전 내용: 
*/

#include <stdio.h>
#include "BinaryTree.h"

// LL 회전
BTreeNode* RotateLL(BTreeNode* bst)
{
	BTreeNode* pNode; // 부모(parent) 노드
	BTreeNode* cNode; // 자식(chile) 노드

	// pNode와 cNode를 각각 LL회전을 위한 위치를 가리키게 함
	pNode = bst;
	cNode = GetLeftSubTree(pNode);

	// 실제 LL 회전이 수행되는 부분
	ChangeLeftSubTree(pNode, GetRightSubTree(cNode));
	ChangeRightSubTree(cNode, pNode);

	// LL회전에 의해 변경된 루트 노드의 주소 값 반환
	return cNode;
}
// RR 회전
BTreeNode* RotateRR(BTreeNode* bst)
{
	BTreeNode* pNode; // 부모(parent) 노드
	BTreeNode* cNode; // 자식(chile) 노드

	// pNode와 cNode를 각각 RR회전을 위한 위치를 가리키게 함
	pNode = bst;
	cNode = GetRightSubTree(pNode);

	// 실제 RR 회전이 수행되는 부분
	ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
	ChangeLeftSubTree(cNode, pNode);

	// RR회전에 의해 변경된 루트 노드의 주소 값 반환
	return cNode;
}

// LR 회전 -> 1) 부분적 RR회전 2) LL회전
BTreeNode* RotateLR(BTreeNode* bst)
{
	BTreeNode* pNode; // 부모(parent) 노드
	BTreeNode* cNode; // 자식(child) 노드

	// pNode와 cNode를 각각 LR회전을 위한 위치를 가리키게 함
	pNode = bst;
	cNode = GetLeftSubTree(pNode);

	// 실제 LR 회전이 수행되는 부분
	ChangeLeftSubTree(pNode, RotateRR(cNode)); // 1) 부분적 RR회전
	return RotateLL(pNode); // 2) LL회전
}
// RL 회전 -> 1) 부분적 LL회전 2) RR회전
BTreeNode* RotateRL(BTreeNode* bst)
{
	BTreeNode* pNode; // 부모(parent) 노드
	BTreeNode* cNode; // 자식(child) 노드

	// pNode와 cNode를 각각 LR회전을 위한 위치를 가리키게 함
	pNode = bst;
	cNode = GetRightSubTree(pNode);

	// 실제 LR 회전이 수행되는 부분
	ChangeRightSubTree(pNode, RotateLL(cNode)); // 1) 부분적 LL회전
	return RotateRR(pNode); // 2) RR회전
}

// 트리의 높이(height)를 계산
int GetHeight(BTreeNode* bst)
{
	int left_h; // 왼쪽의 높이
	int right_h; // 오른쪽의 높이

	// 재귀의 탈출 조건
	if (bst == NULL) // 단말 노드라면
		return 0; // 0을 반환

	// 재귀적 구조를 이용하여 높이를 계산
	left_h = GetHeight(GetLeftSubTree(bst));
	right_h = GetHeight(GetRightSubTree(bst));

	// 큰 값의 높이를 반환
	// 재귀적인 구조이므로 반환하면서 1씩 증가
	if (left_h > right_h)
		return left_h + 1;
	else
		return right_h + 1;
}

// 두 서브 트리의 높이의 차이를 계산
int GetHeightDiff(BTreeNode* bst)
{
	int lsh; // left sub tree height
	int rsh; // right sub tree height

	if (bst == NULL) // 트리에 노드가 없다면
		return 0; // 0을 반환

	lsh = GetHeight(GetLeftSubTree(bst));
	rsh = GetHeight(GetRightSubTree(bst));

	return lsh - rsh; // 균형 인수 계산 결과 반환

}

// 트리의 균형을 잡는 함수
BTreeNode* Rebalance(BTreeNode** pRoot)
{
	int hDiff = GetHeightDiff(*pRoot); // 균형 인수 계산 결과

	// 균형 인수가 +2 이상이라면 LL 또는 LR 상태
	if (hDiff > 1) // 왼쪽 서브 트리 방향으로 높이가 2이상 차이가 난다면
	{
		// 왼쪽 서브 트리의 균형 인수를 확인한다
		if (GetHeightDiff(GetLeftSubTree(*pRoot)) > 0)
			*pRoot = RotateLL(*pRoot); // +1 이상이라면 LL 상태
		else
			*pRoot = RotateLR(*pRoot); // -1 이하라면 LR 상태
	}

	// 균형 인수가 -2 이하라면 RR 또는 RL 상태
	if (hDiff < -1) // 오른쪽 서브 트리 방향으로 높이가 2이상 차이가 난다면
	{
		// 오른쪽 서브 트리의 균형 인수를 확인한다
		if (GetHeightDiff(GetRightSubTree(*pRoot)) < 0)
			*pRoot = RotateRR(*pRoot); // -1 이하라면 RR 상태
		else
			*pRoot = RotateRL(*pRoot); // +1 이상이라면 RL 상태
	}

	return *pRoot;
}

 

나머지 코드는 주석 부분에 설명을 상세히 달아두었다.

코드를 보다가 모르겠으면 다시 책을 보는 것으로.